1 クロス集計表において、セルの度数の比がすべての行で等しい場合、そのクロス集計表の2変数間には関連がない。
2 クロス集計表において、2変数間の関連をみる場合、行パーセント、列パーセントのどちらを示しても、得られる情報に変わりはない。
3 クロス集計表では、2変数間の関連をみることができるが、3変数以上の関連についてみることはできない。
4 度数分布表における相対度数とは、度数を合計した値を各カテゴリーの値で割って算出したものである。
5 連続変数では、値が連続的に変化するため、度数分布表を作成することができない。
選択肢1について
正しいです。文章だとわかりづらいので、具体的な数字で考えてみましょう。「セルの度数の比がすべての行で等しい」クロス集計表(架空のデータです)を用意しました。
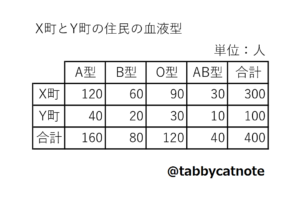
1行目(X町の行)のセルの度数の比は120:60:90:30=4:2:3:1です。
2行目(Y町の行)のセルの度数の比は40:20:30:10=4:2:3:1です。
すなわち、セルの度数の比はすべての行で等しい(すべて4:2:3:1)ですね。
これがどういうことかというと、X町の人でもY町の人でも、全体の40%の人がA型、20%の人がB型、30%の人がO型、10%の人がAB型だという構成割合が同じだということです。もしこういうデータが出てきたら、このクロス集計表の2変数「住んでいる場所」と「血液型」には関連がないと考えられます。
選択肢2について
上記の同じ表で、X町の行パーセントは、A型40%、B型20%、O型30%、AB型10%です。X町の人のうちでそれぞれの血液型の人の割合を示しています。一方、A型の列パーセントは、X町の人75%、Y町の人25%で、A型の人のうちでX町の人とY町の人の割合を示しています。行パーセントと列パーセントでは、得られる情報が違います。選択肢2は誤りです。
選択肢3について
上記の表は、「住んでいる場所」と「血液型」という2変数の関連をみていますが、さらに「性別」も加えた3変数の表も作ることができます。例えば次のような表です(架空のデータです)。

選択肢3は誤りです。
選択肢4について
度数分布表における相対度数とは、各カテゴリーの値を、度数を合計した値で割って算出したものです。選択肢4は誤りです。
選択肢5について
連続変数でも、度数分布表を作成することはできます。選択肢5は誤りです。
正答1